ПОЛЕЗНО Candle: реализация мечты

[Vlad-I-Mir]

Разрешение - всё...

оффтоп

 

[blny]

Под Линукс, эта версия тоже не видит камеру.. пока еще не разобрался в чем дело

На всякий случай, если кому то понадобится.. под Линукс, я проблему решил.. сам собирал, сам и накосячил.
Положил plugin не в ту директорию при инсталяции

Переложил libcameraplugin.so в Candle-1.2.15b/plugins/camera/plugins и все заработало

 

[vvv1234]

P.S. Если удасться сделать ввод с цифрового индикатора в PC - сделаю более детальные измерения.

Ввод с индикатора сделал. Теперь можно сравнить более детально качество работы по карте для двух алгоритмов интерполяции: бикубического и треугольного.

Условия эксперимента.
Заготовка: FR4
Карта: 100х10мм, шаг пробника - 10мм, ячейка интерполяционной сетки - 1х1мм.

Индикатор ставится на 3018 и медленно (1мм/сек) ездит вдоль оси Х от 0 до 100мм. Индикатор регистрирует высоту по Z через каждые 1мм, и эти данные записываются в файл.

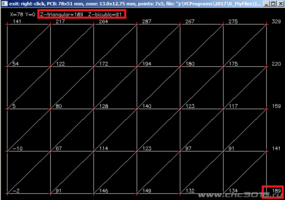
1. Проход по нижней линии (Y=0мм). Белая кривая - без интерполяции, зеленая - треугольная интерполяция, красная - бикубическая. Оба алгоритма работают, разницу высот компенсируют.


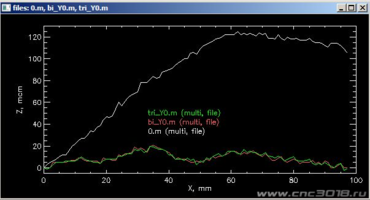2. Более детальный график прохода по нижней линии (Y=0мм), сравнивающий два алгоритма интерполяции. Для случая, когда глубина реза = 40мкм (0.04мм). Пунктирной линией показана поверхность заготовки. Оба алгоритма работают примерно одинаково. Видно, что будет недорезать. Недорез в среднем - около 5мкм (в пределах ошибки измерений), но в максимуме может достигать 20мкм.


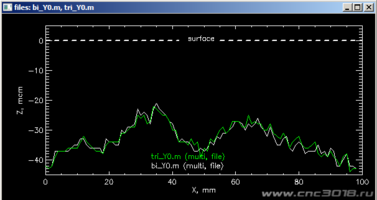3. Проход по средней линии (Y=5мм). Здесь похуже, недорез в среднем - около 20мкм, в максимуме - около 30мкм.


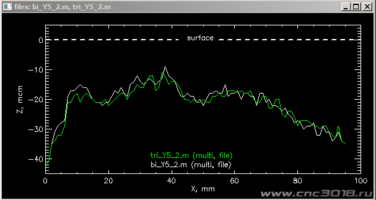Выводы.
1. Лучше перерезать, чем недорезать. Поэтому глубину реза для ПП надо выбирать на 20-30мкм больше, чем толщина фольги.
2. Оба алгоритма интерполяции работают примерно одинаково, разница - в пределах ошибок измерений.
3. Единственное преимущество алгоритма треугольной интерполяции - работает раз в 10 быстрее бикубической. Для программ на PC это не критично. Тогда как для МК, если делать коррекцию по карте в реальном времени - это существенное преимущество.

 

[vvv1234]

Поглубже вник у алгоритм бикубической интерполяции. И сразу появились вопросы, связанные с краевыми эффектами.
Представим, что у нас есть заготовка 80х80мм и ее карта 4х4 точки. Надо посчитать интерполяцию в точку х,у, которая находится в правом нижнем углу заготовки.

Для кубического интерполирования нужны значения пробника в 16 точках, окружающих зону. Но для краевых зон часть этих точек не существует. Поэтому Кэндл назначает эти значения исскуственно, беря их из ближайших известных точек. Т.е для краевых зон эта интерполяция не только неравномерна, но и истинность ее результатов непредсказуема.

Теперь рабочий пример: реальная карта ПП 78х51мм, 7х5 точек.

Сравнение результатов треугольной и бикубической интерполяции для нижнего правого угла заготовки. Критерий правильности простой: в точках пробника результаты интерполяции должны совпадать с измерениями пробника. Измерения пробника показаны в микронах цифрами вблизи углов зон. Результаты интерполяций показаны вверху в красном прямоугольнике.


Выводы.
Результаты треугольной интерполяции совпадают с реальной картой (189мкм).
Результаты бикубической интерполяции отличаются от реальных на 98мкм (189-91). А на практике это большой недорез. Т.е. вблизи правого нижнего угла фреза будет ходить по воздуху.

 

[val013]

Пытаю крайнюю версию в функционале измерений. Ну ничо так, можно пользоваться, если привыкнешь правильно предварительные параметры вводить
Но после родимой 1.1.7, вот подскажите, плз., функционал кнопок "сон", "дверь" и "охлаждение" - как это на практике пользовать можно. Как бы вроде названия понятные, а как это для текущего 3018 - не очень. Ну вот "дверь", как я понимаю - это возможность контроля какого то концевика по какому то пину, а "охлаждение" - это включение какого то конкретного пина?
Кнопку "сон" вообще не понял, ибо после нажатия, выхода из этого режима не увидел, кроме как сбросом с соответствующей потерей рабочих координат.
И еще, не заметил тут весьма полезных(может только лично мне) кнопок сохранения позиции и возврата к оной, что имелось в 1.1.7. Временно не предусмотрена, нафиг не надо, или по другому реализовано?

 

[OlegK]

Кнопку "сон" вообще не понял, ибо после нажатия, выхода из этого режима не увидел, кроме как сбросом с соответствующей потерей рабочих координат.

Так и задумано автором ГРБЛ

$SLP - Enable Sleep Mode

This command will place Grbl into a de-powered sleep state, shutting down the spindle, coolant, and stepper enable pins and block any commands. It may only be exited by a soft-reset or power-cycle.

 

[val013]

Так и задумано автором ГРБЛ

Это понятно, в принципе, даже на басурманском Вопрос - какая практическая пользительность от сей возможности. Пока не удалось осознать до всей глубины внутреннего восприятия на уровне "это надо и без этого сапсем плёхо"

 

[OlegK]

Пока не удалось осознать

Это потому, что нафик оно никому не нужно...

Ваши сообщения автоматически объединены: 05.02.2023

Вопрос - какая практическая пользительность от сей возможности.

Не, если там дальше почитать, то пользительность какая-никакая прослеживается -

This feature is useful if you need to automatically de-power everything at the end of a job by adding this command at the end of your g-code program, BUT, it is highly recommended that you add commands to first move your machine to a safe parking location prior to this sleep command. It also should be emphasized that you should have a reliable CNC machine that will disable everything when its supposed to, like your spindle. Grbl is not responsible for any damage it may cause. It's never a good idea to leave your machine unattended. So, use this command with the utmost caution!

Но вот зачем в программе такая кнопка - загадка...

 

[val013]

Это потому, что нафик оно никому не нужно...

Но вот зачем в программе такая кнопка - загадка...

Ну дык, душа то просит - есть кнопка, значить надо! И хочецца нажать. Ладно - нажимаешь. А чем это отличаецца от тупо выключения питания? Потому опять хочецца - таперича понять, зачем оно придумато

оффтоп

 

[serg1967]

Ну дык, душа то просит - есть кнопка, значить надо! И хочецца нажать. Ладно - нажимаешь. А чем это отличаецца от тупо выключения питания? Потому опять хочецца - таперича понять, зачем оно придумато

оффтоп

как в рекламе Эндер3 - возможность допечати модели после выключения электричества. Модель то отклеилась(

 

[demyuri]

оффтоп

в последнем слове буква "Н" лишняя

оффтоп

 

[val013]

как в рекламе Эндер3 - возможность допечати модели после выключения электричества. Модель то отклеилась(

Про рекламу Эндер3 не ведаю, но ещё раз вопрошу - "чем это отличаецца от тупо выключения питания", если потом дальнейшие вынужденные манипуляции сбрасывают рабочие координаты, а "кнопок сохранения позиции и возврата к оной" не имеется в наличии.
Может туплю(быстрее всего), но не доходит

в последнем слове буква "Н" лишняя

Наташа подтверждает- обшиблося немношко

оффтоп

 

[Vlad-I-Mir]

...

Ваши сообщения автоматически объединены: 05.02.2023

Не, если там дальше почитать, то пользительность какая-никакая прослеживается -

Но вот зачем в программе такая кнопка - загадка...

Фишка этой кнопки в следующем: Итак, используйте эту команду с предельной осторожностью!

 

[Alexmit]

а "охлаждение" - это включение какого то конкретного пина?

Да, в Ардуиновском исчислении A3 (в процессорном PORT C BIT 3). Включается по команде M8.
Можно ещё использовать A4 по команде M7, но это надо в исходниках разрешить.
Используется в основном с лазерами.
Лазерный станок, выбор. * ФОРУМ О СТАНКАХ CNC 3018

 

[vvv1234]

Выяснил, почему в Candle при работе с картой иногда фреза начинает ходить по воздуху. Дело в том, что начальная точка карты всегда зануляется. А рабочая координата по Z в этой точке остается без изменения. Поэтому, чтобы избежать хождение по воздуху, после съема карты надо вернуть фрезу в начальную точку, опустить до касания с заготовкой и занулить рабочую Z-координату.

Я это поправил, когда доделаю контурную карту в Candle-Tools - выложу.